平成27年度(2015) 試験 問14 | 中小企業診断士 経済学・経済政策

いま、２つの財、財Ｘ1と財Ｘ2を消費可能な個人の効用最大化行動を考える。
当該の個人は、所得80を有し、財Ｘ1の価格は２、財Ｘ2の価格は４という条件のもとで、効用が最大になるよう財Ｘ1の消費量ｘ1と財Ｘ2の消費量ｘ2とを組み合わせることができる。
この個人の効用関数はＵ＝ｘ1ｘ2と与えられており、合理的な当該個人は、ｘ1＝20、ｘ2＝10という組み合わせを選択することが分かっている。
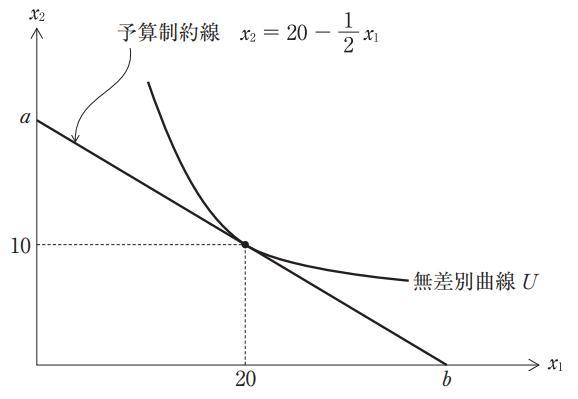
下図では、縦軸の切片ａと横軸の切片ｂとを結ぶ予算制約線と無差別曲線Ｕの接点として、効用最大化の行動が図示されている。

この状況を説明する記述として、最も適切なものを下記の解答群から選べ。